This year's Google CTF, while traveling in Danang, I managed to solve 2 misc problems: npc and symatrix. Both seem like algorithm-flavored problems.

Here are the writeups for them:

npc

Problem description

A friend handed me this map and told me that it will lead me to the flag. It is confusing me and I don't know how to read it, can you help me out?

Attachment

Analysis

We got the following 4 files after extracting the problem archive:

• encrypt.py: Main code for encryption

• secret.age: Encrypted data

• hint.dot: Hints for finding the plaintext

• USACONST.TXT: Dictionary

Skim through the flow of encrypt.py, I found the interesting parts that describe:

• Encryption mechanism: Using pyrage.passphrase :

    from pyrage import passphrase
  
    with open(filename, 'wb') as f:
        f.write(passphrase.encrypt(secret, password))
  

• Wordlist generation: Unique normalized words from USACONST.TXT

    def get_word_list():
      with open('USACONST.TXT', encoding='ISO8859') as f:
        text = f.read()
      return list(set(re.sub('[^a-z]', ' ', text.lower()).split()))
  

• Password generation: Random words from word list:

    def generate_password(num_words):
      word_list = get_word_list()
      return ''.join(secrets.choice(word_list) for _ in range(num_words))
  

• Hint generation for hint.dot file:

    def generate_hint(password):
      random = secrets.SystemRandom()
      id_gen = IdGen()
      graph = Graph([],[])
  
      # Step 1: Append original graph edges
      for letter in password:
        graph.nodes.append(Node(letter, id_gen.generate_id()))
  
      # Edges that represent the relationship between 2 consecutive characters
      for a, b in zip(graph.nodes, graph.nodes[1:]):
        graph.edges.append(Edge(a, b))
  
      # Step 2: Add random (and maybe non-existence) edges to confuse us
      for _ in range(int(len(password)**1.3)):
        a, b = random.sample(graph.nodes, 2)
        graph.edges.append(Edge(a, b))
  
      # Step 3: Shuffle the edges, nodes and connections to further confuse us
      random.shuffle(graph.nodes)
      random.shuffle(graph.edges)
      for edge in graph.edges:
        if random.random() % 2:
          edge.a, edge.b = edge.b, edge.a
  
      return graph
  

From the above information, I can already imagine the encryption and hint generation process:

1. Generate word list

2. Generate a password by picking random words from the word list

3. Use the generated password to encrypt the flag and write to secret.age

4. Generate the graph containing the hint from the password and write to hint.dot file

So what is the problem that we need to solve given the following process?

To get the encryption password, we will need to solve process 4 and recover the password from the given obfuscated graph.

It's clear that if they didn't add the random and shuffling part of the code, then we would be dealing with the edges of a degenerated graph.

But after the obfuscation process, here is what we get from hint.dot

graph {
    comment="Nodes"
    1051081353 [label=a];
    66849241 [label=a];
    53342583 [label=n];
    213493562 [label=d];
    4385267 [label=i];
    261138725 [label=o];
    51574206 [label=t];
    565468867 [label=e];
    647082638 [label=r];
    177014844 [label=d];
    894978618 [label=e];
    948544779 [label=n];
    572570465 [label=n];
    582531406 [label=r];
    264939475 [label=a];
    415170621 [label=s];
    532012257 [label=t];
    151901859 [label=v];
    346347468 [label=g];
    148496047 [label=g];
    125615053 [label=s];
    723039811 [label=e];
    962878065 [label=i];
    112993293 [label=w];
    748275487 [label=n];
    120330115 [label=s];
    76544105 [label=c];
    186790608 [label=h];

    comment="Edges"
    53342583 -- 565468867;
    582531406 -- 76544105;
    125615053 -- 120330115;
    264939475 -- 572570465;
    53342583 -- 565468867;
    532012257 -- 264939475;
    346347468 -- 532012257;
    125615053 -- 582531406;
    177014844 -- 120330115;
    264939475 -- 962878065;
    comment="<lots more edges>"
}

You can paste the graph data into graphviz, but the result doesn't look fine:

A thing to note is that if a character appears multiple times in the password, they are treated as different nodes. This will help us to build the password from the graph easier because we will not be confused by unnecessary edges.

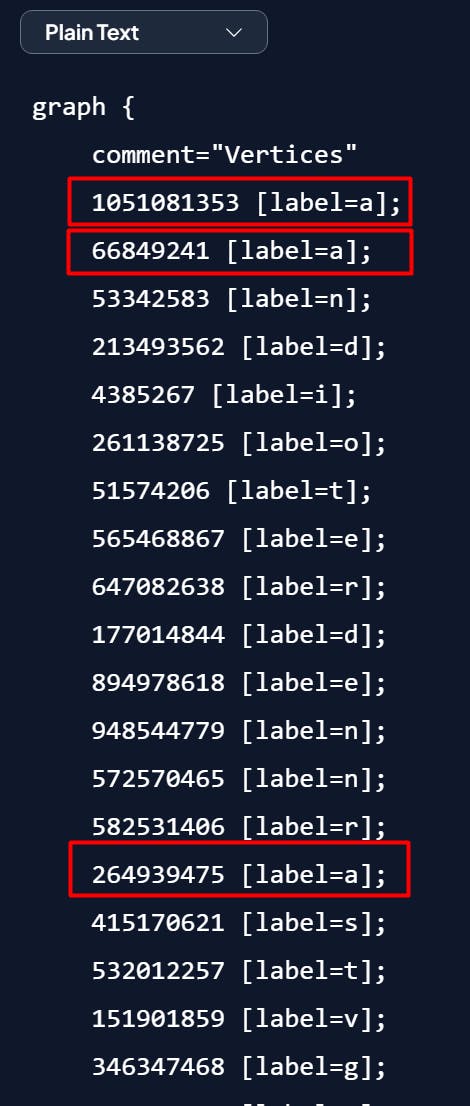
For example, a graph that represents the word "abac" using the method above will be like this:

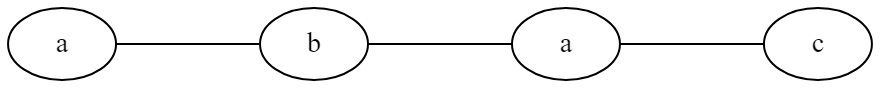
If they don't treat the characters as unique nodes, it will create unnecessary loops like this:

Also because we treated the characters as unique nodes, we knew that the password has 28 characters.

Following the flow of generate_hint function above, if your password is "googlectf", the graph definition would look like this (this is just a demonstration, realistically in the code, the label ids will be randomized so there is no straight way to recover the password):

graph {
    comment="Vertices"
    1 [label=g];
    2 [label=o];
    3 [label=o];
    4 [label=g];
    5 [label=l];
    6 [label=e];
    7 [label=c];
    8 [label=t];
    9 [label=f];

    comment="Edges"
    1 -- 2
    2 -- 3
    3 -- 4
    4 -- 5
    5 -- 6
    6 -- 7
    7 -- 8
    8 -- 9
}

Which visualized to the following:

But after the obfuscation process, it would look kind of this:

And hence after the process, we will lose every of these informations:

• The starting node

• The ordering of nodes (if 2 nodes are connected then which comes first?)

• Which are the real edges?

And the clues that are left:

• This graph contains the connections of all the consecutive characters of the password

• The password has 28 characters

• The password must contain words from the word list

And so, the journey begins

The starting node

I simply try each of the 28 nodes as the starting node

The ordering of nodes

One thing we know is that the text representation of the correct node ordering must exist inside the word list.

Hence we can traverse the graph from the chosen starting node, try each of the ordering possible and check if it matches the word list.

There might be multiple ordering that matches the conditions, so we need to store all of them in an array and then check to see which one correctly decrypt the flag.

Which are the real edges?

Same to the problem of node ordering, the real edges' text representation must exist inside the word list.

Hence we can filter this while checking the ordering.

We also need to filter fake edges that appear in the word list.

Minor word-splitting problem

Since words in the word list were joined without space to form the password, we also need to deal with the problem that one password candidate can be generated from different combinations of words inside the word list.

For example "forever" can be combined from "for" + "ever" or "forever" itself. This case is trivial, but another case that can cause a problem is "generous". It cannot be combined if we choose "gene" + something, but can be combined using the word "generous" itself.

To solve this word-matching problem, I chose the Trie data structure. It provides the ability to conveniently check whether a word exists inside the dictionary. For this particular problem, I optimized it a bit to check where can we jump from the current node of Trie instead of having to repeatedly check the whole word again and again.

Here is my Trie code, generated by ChatGPT

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_end_of_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        current = self.root
        for char in word:
            if char not in current.children:
                current.children[char] = TrieNode()
            current = current.children[char]
        current.is_end_of_word = True

    def has_next_node(self, current_node, char):
        return current_node.children[char] if char in current_node.children else False

Let's implement

After getting every puzzle piece in hand, I built my tryToSolve function which is simply a backtracking function to try each possible ordering of nodes and picking out the candidates:

marked = {}

def tryToSolve(u, trieNode = trie.root, len = 28):
    nodeid, char = nodes[u]
    nextNode = trie.has_next_node(trieNode, char)

    res = []

    if not nextNode:
        if trieNode.is_end_of_word:
            return tryToSolve(u, trie.root, len)
        return []

    len -= 1

    marked[nodeid] = True

    # print(u, char)

    if len == 0:
        return [char]

    for v in adj[nodeid]:
        if not v in marked:
            possiblities = tryToSolve(v, nextNode, len)
            for possibility in possiblities:
                res.append(char + possibility)

    del marked[nodeid]

    return res

And of course, I ran the function with each node as the starting one, as described earlier:

for startingNode in nodes.values():
    marked = {}
    for word in tryToSolve(startingNode[0], trie.root, 28):
        print(word)

After execution, I got 6 possible candidates:

┌──(kali㉿kali)-[~/Desktop/npc]
└─$ python3 solve.py                                                                                              130 ⨯
dwatersigngivenchosenstandar
givenstandardsignwaterchosen
signgivenstandardwaterchosen
waterchosenstandardsigngiven
standardwatersigngivenchosen
chosenstandardwatersigngiven

And the rest is easy. I just need to try each one for decryption.

from pyrage import passphrase

encrypted = open('secret.age', 'rb').read()

candidates = open('candidates.txt').readlines()
for pw in candidates:
    try:
        pw = pw.strip()
        print(passphrase.decrypt(encrypted, pw))
    except Exception as e:
        print(e)

┌──(kali㉿kali)-[~/Desktop/npc]
└─$ python3 solve1.py
Decryption failed
Decryption failed
Decryption failed
Decryption failed
b'CTF{S3vEn_bR1dg35_0f_K0eN1g5BeRg}'
Decryption failed

Flag

CTF{S3vEn_bR1dg35_0f_K0eN1g5BeRg}

Darn it, we were still the second team to solve it :(

symatrix

Problem description:

The CIA has been tracking a group of hackers who communicate using PNG files embedded with a custom steganography algorithm. An insider spy was able to obtain the encoder, but it is not the original code. You have been tasked with reversing the encoder file and creating a decoder as soon as possible in order to read the most recent PNG file they have sent.

Attachment

Analysis

We got the following 4 files after extracting the problem archive:

• encoder.c: Main code for encoding

• symatrix.png: Encoded data

Upon inspection of encoder.c, I realized that it's a C file compiled from Python code:

I tried to compile it using gcc but it threw lots of errors:

When inspecting further, I found out that there are blocks of original python code left in the compiled source. By further searching, I found 70 of those blocks.

I managed to extract those Python code blocks, but they still look like about 500 lines of a mess:

/* "encoder.py":5
 * import binascii
 * 
 * def hexstr_to_binstr(hexstr):             # <<<<<<<<<<<<<<
 *     n = int(hexstr, 16)
 *     bstr = ''
 */
/* "encoder.py":6
 * 
 * def hexstr_to_binstr(hexstr):
 *     n = int(hexstr, 16)             # <<<<<<<<<<<<<<
 *     bstr = ''
 *     while n > 0:
 */
/* "encoder.py":7
 * def hexstr_to_binstr(hexstr):
 *     n = int(hexstr, 16)
 *     bstr = ''             # <<<<<<<<<<<<<<
 *     while n > 0:
 *         bstr = str(n % 2) + bstr
 */
...

And so I threw them into ChatGPT to see what it can do:

And out of my astonishment, I received the beautifully formatted,

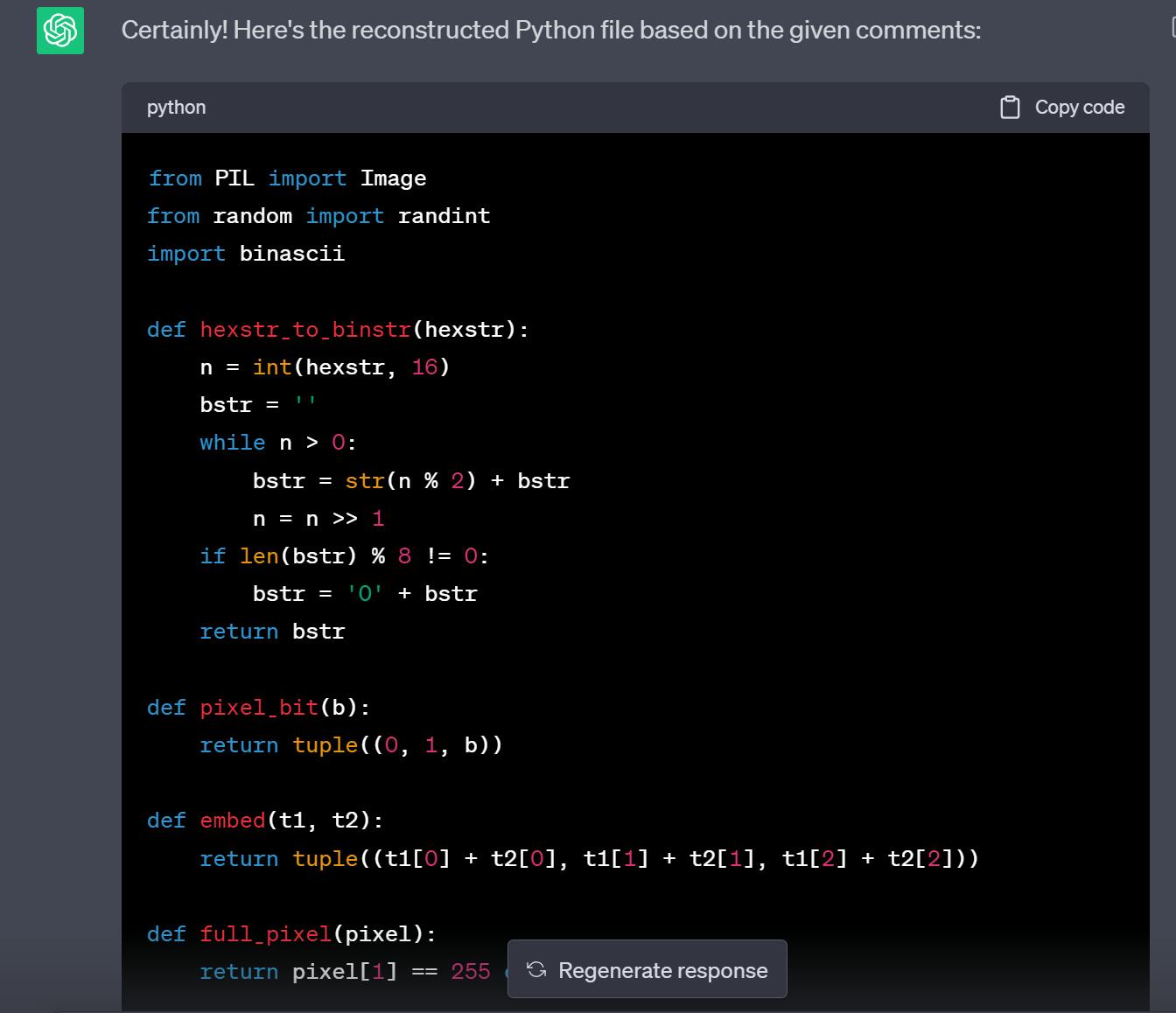
So, what do we need to see?

The encoder's source code

Now we got the encoder source code:

from PIL import Image
from random import randint
import binascii

def hexstr_to_binstr(hexstr):
    n = int(hexstr, 16)
    bstr = ''
    while n > 0:
        bstr = str(n % 2) + bstr
        n = n >> 1
    if len(bstr) % 8 != 0:
        bstr = '0' + bstr
    return bstr

def pixel_bit(b):
    return tuple((0, 1, b))

def embed(t1, t2):
    return tuple((t1[0] + t2[0], t1[1] + t2[1], t1[2] + t2[2]))

def full_pixel(pixel):
    return pixel[1] == 255 or pixel[2] == 255

print("Embedding file...")

bin_data = open("./flag.txt", 'rb').read()
data_to_hide = binascii.hexlify(bin_data).decode('utf-8')

base_image = Image.open("./original.png")
x_len, y_len = base_image.size

nx_len = x_len * 2

new_image = Image.new("RGB", (nx_len, y_len))
base_matrix = base_image.load()
new_matrix = new_image.load()

binary_string = hexstr_to_binstr(data_to_hide)
remaining_bits = len(binary_string)

nx_len = nx_len - 1
next_position = 0

for i in range(0, y_len):
    for j in range(0, x_len):
        pixel = new_matrix[j, i] = base_matrix[j, i]
        if remaining_bits > 0 and next_position <= 0 and not full_pixel(pixel):
            new_matrix[nx_len - j, i] = embed(pixel_bit(int(binary_string[0])), pixel)
            next_position = randint(1, 17)
            binary_string = binary_string[1:]
            remaining_bits -= 1
        else:
            next_position -= 1

new_image.save("./symatrix.png")
new_image.close()
base_image.close()

print("Work done!")
exit(1)

The encoding process

1. The encoder doubled the image width:

    nx_len = x_len * 2
    new_image = Image.new("RGB", (nx_len, y_len))
   

2. It hides one bit of data. The original (r, g, b) code turned into (r, g + 1, b + encrypted_bit). The encrypted pixel lies in the doubled half of the image ([j, i] -> [nx_len - j, i])

    def pixel_bit(b):
        # Encoding formla
        return tuple((0, 1, b))
   
    def embed(t1, t2):
        return tuple((t1[0] + t2[0], t1[1] + t2[1], t1[2] + t2[2]))
   
    def full_pixel(pixel):
        return pixel[1] == 255 or pixel[2] == 255
   
    if remaining_bits > 0 and next_position <= 0 and not full_pixel(pixel):
        new_matrix[nx_len - j, i] = embed(pixel_bit(int(binary_string[0])), pixel)
   

3. It chooses another random position for hiding the next bit:

    next_position = randint(1, 17)
   

Solution

So now we just need to write a simple script to find the encoded bits and get the flag

from PIL import Image

def decode_image(encoded_image_path):
    encoded_image = Image.open(encoded_image_path)
    encoded_matrix = encoded_image.load()

    decoded_data = ""

    x_len, y_len = encoded_image.size
    nx_len = x_len // 2

    for i in range(y_len):
        for j in range(nx_len):
            [r1, g1, b1] = encoded_matrix[j, i]
            [r2, g2, b2] = encoded_matrix[x_len - j - 1, i]

            if r1 == r2 and g1 + 1 == g2 and b2 - b1 <= 1:
                # print((r1, g1, b1))
                # print((r2, g2, b2))
                decoded_data += str(b2 - b1)

    decoded_bytes = bytearray()

    for i in range(0, len(decoded_data), 8):
        byte_str = decoded_data[i:i+8]
        decoded_bytes.append(int(byte_str, 2))

    return decoded_bytes

print(decode_image('./symatrix.png'))

Flag

CTF{W4ke_Up_Ne0+Th1s_I5_Th3_Fl4g!}

GLHF!

Thank you vh++ for hosting a team for Vietnamese